We present an adaptive multilevel Monte Carlo (MLMC) method for weak approximations of solutions to Itˆo stochastic differential equations (SDE). The work [Oper. Res. 56 (2008), 607–617] proposed and analyzed an MLMC method based on a hierarchy of uniform time discretizations and control variates to reduce the computational effort required by a single level Euler–Maruyama Monte Carlo method from
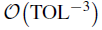
to
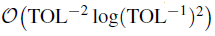
for a mean square error of
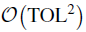
. Later, the work [Lect. Notes Comput. Sci. Eng. 82, Springer, Berlin, 2012, 217–234] presented an MLMC method using a hierarchy of adaptively refined, non uniform time discretizations, and, as such, it may be considered a generalization of the uniform time discretization MLMC method.
This work improves the adaptive MLMC algorithms presented in [Lect. Notes Comput. Sci. Eng. 82, Springer, Berlin, 2012, 217–234] and it also provides mathematical analysis of the improved algorithms. In particular, we show that under some assumptions our adaptive MLMC algorithms are asymptotically accurate and essentially have the correct complexity but with improved control of the complexity constant factor in the asymptotic analysis. Numerical tests include one case with singular drift and one with stopped diffusion, where the complexity of a uniform single level method is
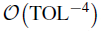
For both these cases the results confirm the theory, exhibiting savings in the computational cost for achieving the accuracy
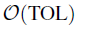
from
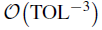
for the adaptive single level algorithm to essentially
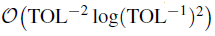
for the adaptive MLMC algorithm.
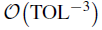 to
to 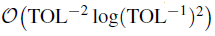 for a mean square error of
for a mean square error of 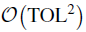 . Later, the work [Lect. Notes Comput. Sci. Eng. 82, Springer, Berlin, 2012, 217–234] presented an MLMC method using a hierarchy of adaptively refined, non uniform time discretizations, and, as such, it may be considered a generalization of the uniform time discretization MLMC method.
. Later, the work [Lect. Notes Comput. Sci. Eng. 82, Springer, Berlin, 2012, 217–234] presented an MLMC method using a hierarchy of adaptively refined, non uniform time discretizations, and, as such, it may be considered a generalization of the uniform time discretization MLMC method.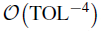 For both these cases the results confirm the theory, exhibiting savings in the computational cost for achieving the accuracy
For both these cases the results confirm the theory, exhibiting savings in the computational cost for achieving the accuracy 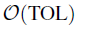 from
from 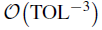 for the adaptive single level algorithm to essentially
for the adaptive single level algorithm to essentially 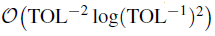 for the adaptive MLMC algorithm.
for the adaptive MLMC algorithm.