Motivation and objectives
Experimental design is an important topic in engineering and sciences that pertains to model calibration, validation, and predictive modeling. As physical models are becoming increasingly more complex, the evaluation of corresponding utility values and the optimization procedure in the design of an experiment are becoming computationally intensive. Techniques such as sparse quadrature, surrogate modeling, model reduction, and asymptotic approximation have been applied to the design of experiments. Research activities on the subject have recently gained momentum due to the current trend to carry out large-scale PDE related experimental designs within a Bayesian framework.
Methodology
In our current project, we are developing and analyzing fast experimental design methodologies based on innovative Laplace methods. We provide fast asymptotic results and explore the intrinsic system sparsity for the numerical integration of the expected post-experimental information gain, in both determined and ill-conditioned systems. Based on this, we propose the most efficient design setup.
Results and ongoing work
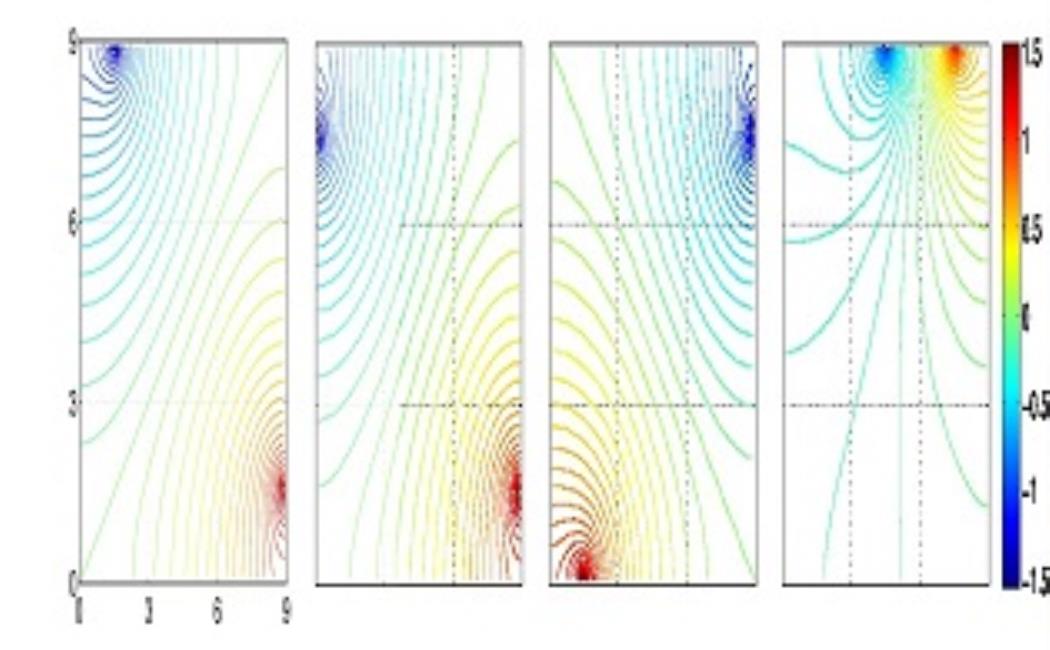
We are also applying our methodology to a wide range of engineering applications, such as high pressure shock tube experiments and impedance tomography. The following figures show the optimal current pattern (left), the worst current pattern (right) and two current patterns with intermediate information gains. The uncertainties of the conductivities along the diagonal (top-left to bottom-right) are assumed to be higher than those in the rest of the square domain.
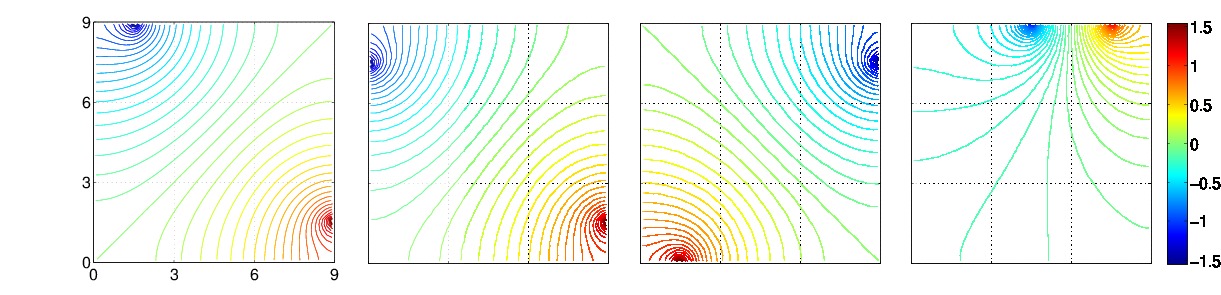
Two examples of current patterns inducing the highest information gains. Two examples of current patterns inducing the low information gains.
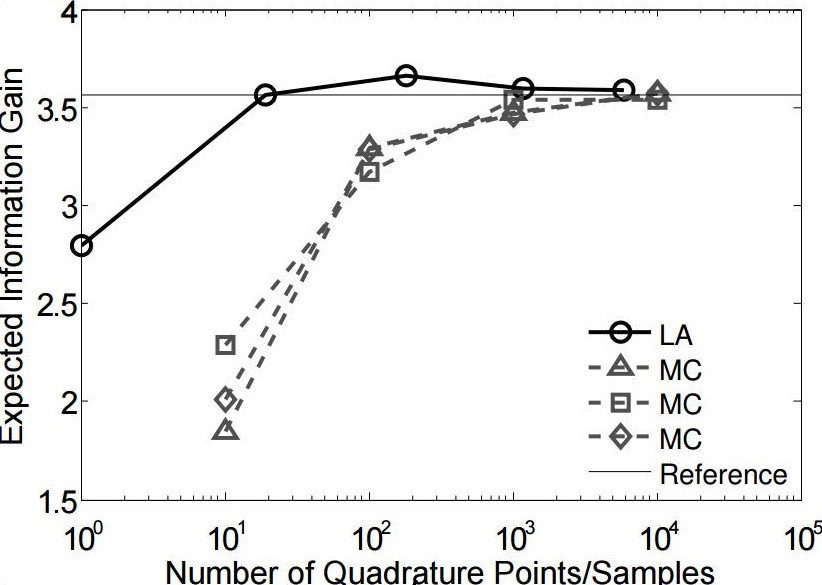
The performance of our method compared with double-loop Monte Carlo:
Parallel to methodology development, we are currently working with an extensive team of experimentalists and engineers on the experimental design of combustion in shock tube. The inference of reactive rate function for the oxidation of hydrogen is one of the experiments we are considering. The first picture below shows the expected information gain increases as the temperature and the initial concentration of hydrogen increases. The second picture visualizes the expected information gain for two experiments carried out using two different temperatures and a single iniitial concentration of hydrogen. The maximum information gain is obtained at the point where two temperatures are well-seperated. The third picture shows three iso-surfaces of the expected information gain in a series of experiments where the temperatures are different and the initial concentration of hydrogen is fixed as the maximum.
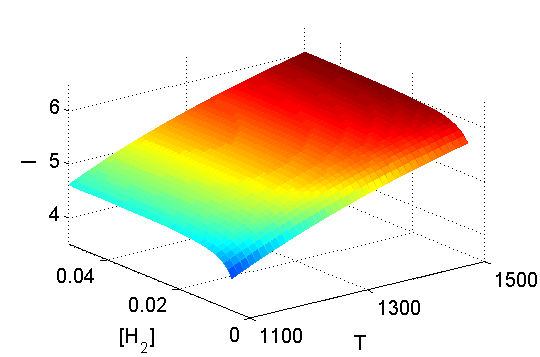
The expected information gain with respect to the initial temperature and initial hydrogen concentration.
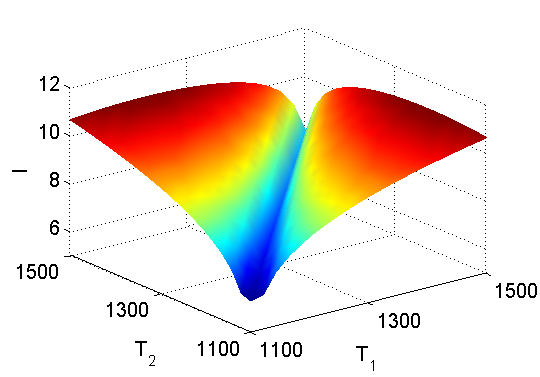
The expected information gain with respect to two temperatures, while the initial hydrogen concentration is a constant (0.05).
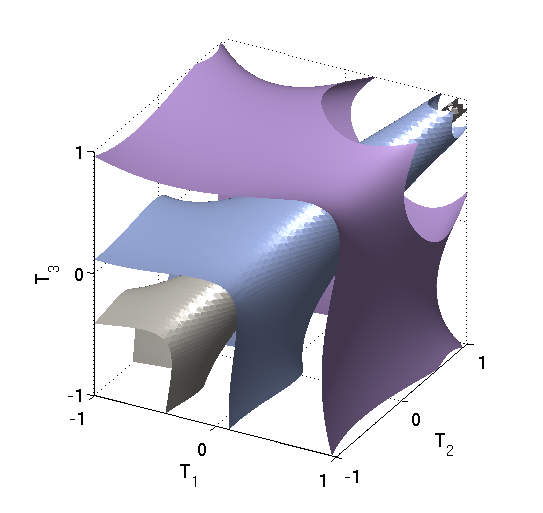
The iso-surface of the expected information gain with respect to three temperatures.
Fast Bayesian optimal experimental design for seismic source inversion, Computer Methods in Applied Mechanics and Engineering, vol. 291, pp. 123-145, 2015