Motivation
Data assimilation, or filtering, refers to the problem of combining noisy observations of a (typically physical) system together with a model for that system in order to infer the state and/or parameters online as data is received. In the Bayesian probabilistic context of a hidden-Markov model, this leads to a recursion of Bayesian updates. The objective of the filtering problem is then to obtain the posterior distribution of the unknown as a function of the history of observations. One objective of this research is (i) to obtain better approximations of this distribution. This is often not possible in practice even when it is the objective. One may aim to obtain an estimator (and some coarse measure of spread) which tracks the truth rather than aiming for the full distribution. Another objective of this research is (ii) to analyze existing commonly used filtering algorithms from this perspective to determine their accuracy and stability properties. By the triangle inequality such estimators can be related to the mean of the filtering distribution (i) in case this is stable. This is important both for theoreticians in terms of making sense of the results of these filters in a rigorous way, and also for the practitioner who may use insight from these studies to develop better filters.
Methodology
Currently we are developing algorithms for (i) which rely on deterministic parameterizations of the distribution and hence surmount the undesirable convergence rates associated with Monte-Carlo sampling [1]. In order to tackle (ii), we identify properties of the underlying system and leverage these to prove rigorous convergence results for filter estimators. In particular, the methodology relies on observing the unpredictable part of the system, and trusting the observations sufficiently much [2-5].
Outcomes
We have tested and implemented the first of our filters with very promising results [1]. We have rigorous convergence results for the most fundamental filter 3DVAR [2,3,4] and are working on similar results for the more elaborate filters ExKF and EnKF [5].
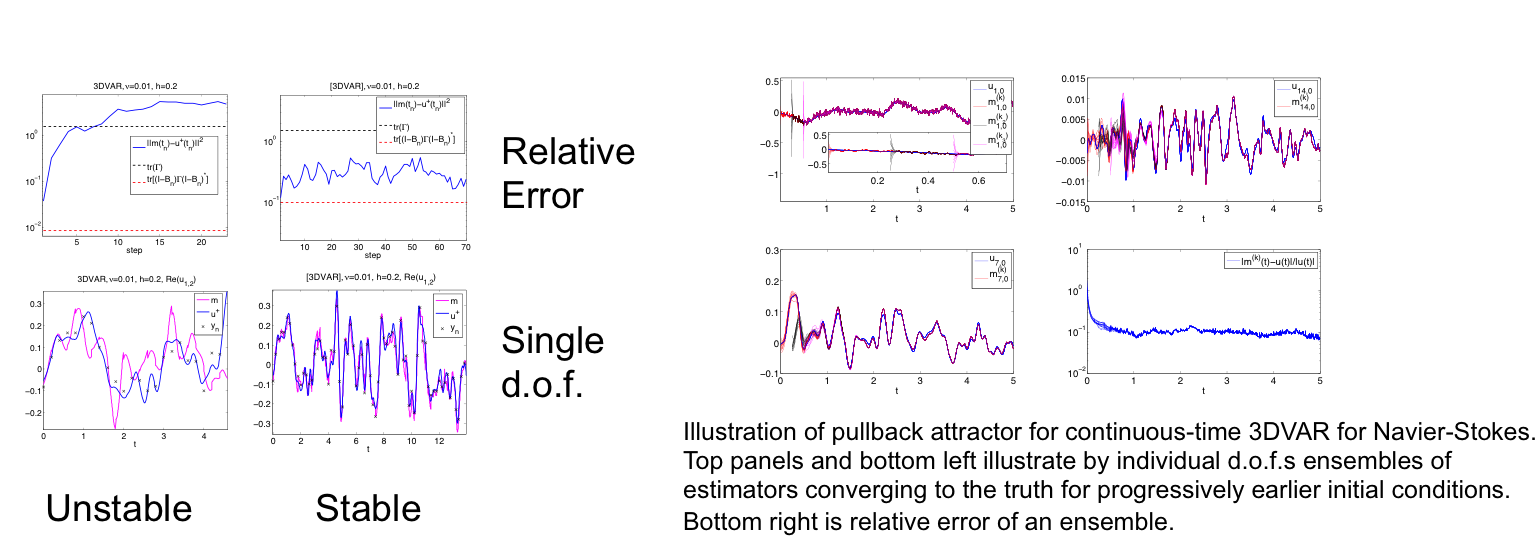


 Accuracy and Stability of Filters for Dissipative PDEs. Physica D 245, 1, 34-45 (2013).
Accuracy and Stability of Filters for Dissipative PDEs. Physica D 245, 1, 34-45 (2013). Accuracy and Stability of The Continuous Time 3DVAR Filter for The Navier-Stokes Equation. Nonlinearity 26 2193 (2013).
Accuracy and Stability of The Continuous Time 3DVAR Filter for The Navier-Stokes Equation. Nonlinearity 26 2193 (2013). Analysis of the 3DVAR Filter for the Partially Observed Lorenz 63 Model. Discrete and Continuous Dynamical Systems A 34 1061-1078 (2014).
Analysis of the 3DVAR Filter for the Partially Observed Lorenz 63 Model. Discrete and Continuous Dynamical Systems A 34 1061-1078 (2014). Well-Posedness And Accuracy Of The Ensemble Kalman Filter In Discrete And Continuous Time. I Nonlinearity 27 2579, 2014.
Well-Posedness And Accuracy Of The Ensemble Kalman Filter In Discrete And Continuous Time. I Nonlinearity 27 2579, 2014.