
Motivation:
Inspired by the recent development of pCN and other function-space MCMC samplers, and also the recent independent development of Riemann manifold methods and stochastic Newton methods, we propose a class of algorithms which combine the benefits of both, yielding various dimension-independent, likelihood-informed (DILI) sampling algorithms. These algorithms are very effective at obtaining minimally-correlated samples from very high-dimensional distributions.
We are currently working on implementing these methods in more real-world applications including the above, as well as seismology, ceanography, finance, green wireless, clean combustion, and many more … In parallel, we are also extending these results to develop more effective samplers, and working on establishing rigorous theoretical convergence properties.
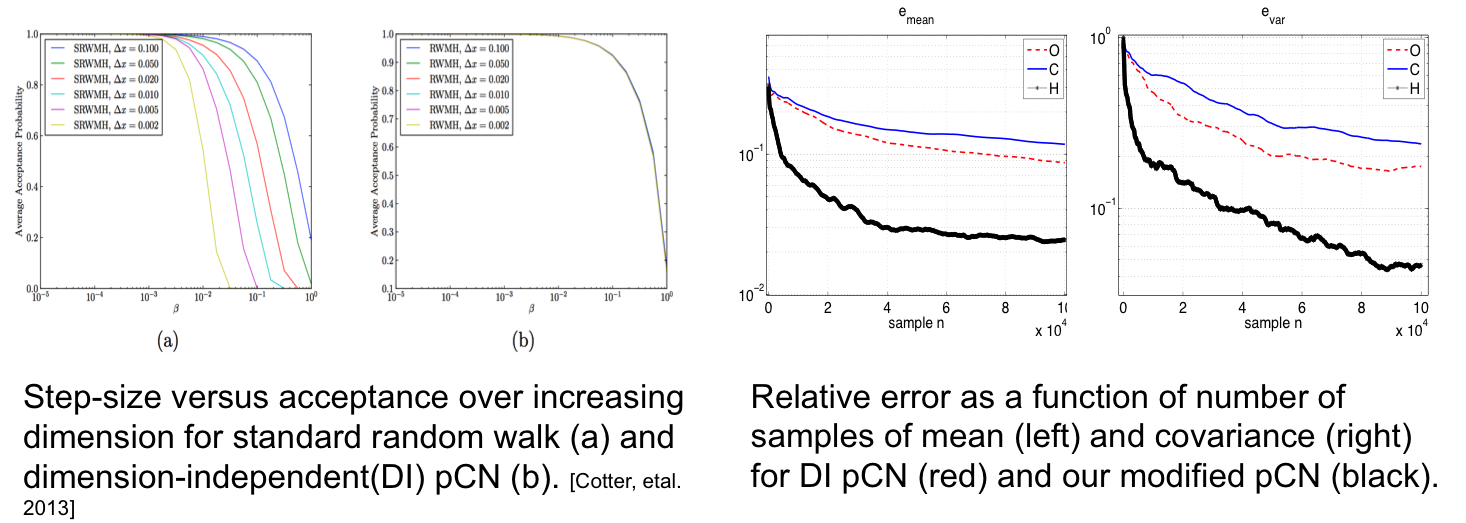
[1] Law, KJH,  Proposals whichspeed-up function-space MCMC. Journal of Computational and Applied Mathematics, 262, 127-138 (2014).
Proposals whichspeed-up function-space MCMC. Journal of Computational and Applied Mathematics, 262, 127-138 (2014).
[2] Cui, T, Law, KJH, Marzouk, Y, Likelihood-informed sampling of Bayesian nonparametric inverse problems. In preparation.
[3] Law, KJH, Stuart, AM, Evaluating Data Assimilation Algorithms. Monthly Weather Review 140(2012), 3757-3782.
[4] Iglesias, MA, Law, KJH, Stuart, AM,  Evaluationof Gaussian approximations for data assimilation in reservoir models Computational Geosciences, 17:5, 851-885 (2013).
Evaluationof Gaussian approximations for data assimilation in reservoir models Computational Geosciences, 17:5, 851-885 (2013).
[5] Cotter, SL, Roberts, GO, Stuart, AM, White, D, MCMC methods for functions: modifying old algorithms to make them faster (Statistical Science, To Appear).