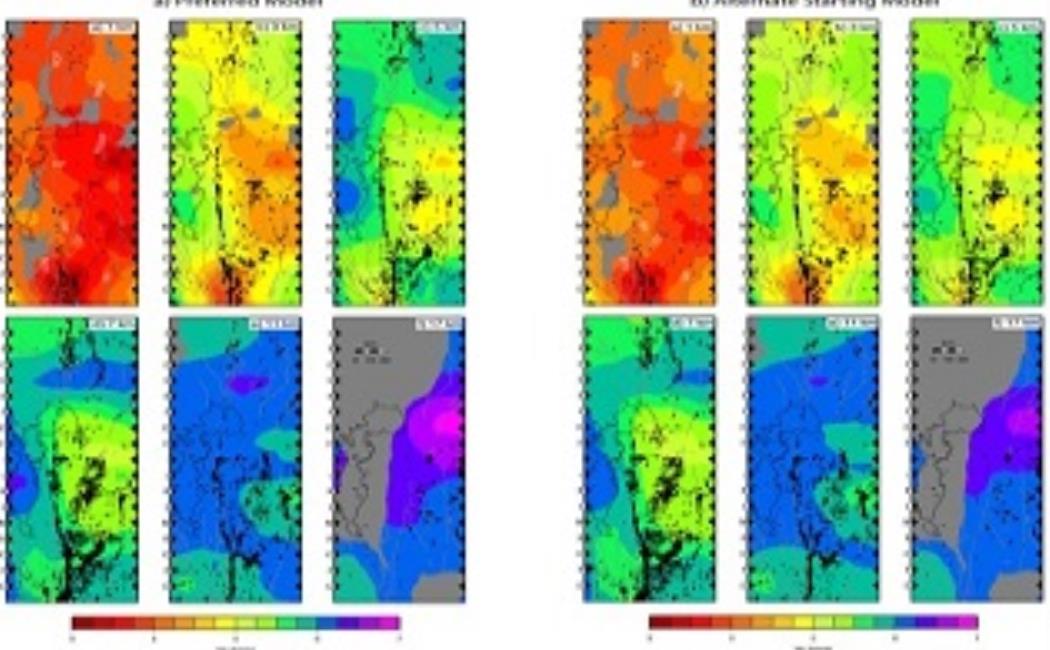
We are developing a new method based on the Bayesian inference technique for the ground motion computations. The ultimate goal of this project is to have a better understanding of earthquake distribution. We are interested in accurately computing quantities of interests, such as spectral acceleration and peak ground acceleration. These quantities will then be used to produce engineering graphs which are employed to design seismic-resistant buildings and structures.
Fast Bayesian optimal experimental design for seismic source inversion, Computer Methods in Applied Mechanics and Engineering, vol. 291, pp. 123-145, 2015.Analysis and Computation of Hyperbolic PDEs with Random Data, Submitted, March 2013.A stochastic collocation method for the second order wave equation with a discontinuous random speed, Numer. Math., Vol. 123, No. 3, p. 493-536, 2013. Analysis and computation of the elastic wave equation with random coefficients, Computers and Mathematics with Applications, Vol. 70, Issue 10, pp. 2454–2473, November 2015.On the Linear Stability of the Fifth-Order WENO Discretization, Journal of Scientific Computing, vol. 47, no. 2, pp. 127-149, 2011.Taylor Expansion and Discretization Errors in Gaussian Beam Superposition, Wave Motion, vol. 47, no. 7, pp. 421-439, 2010.