Multilevel Approximation of Stochastic Reaction Networks

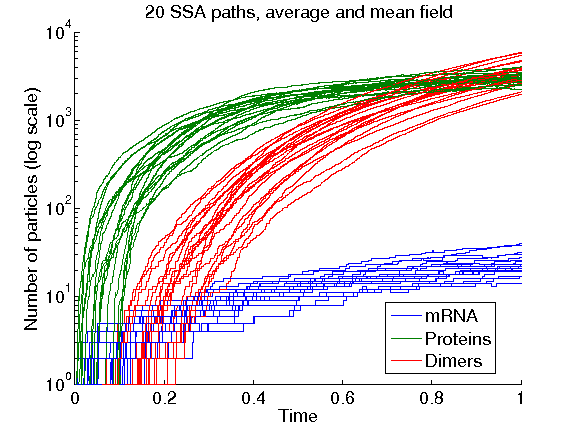
Stochastic Reaction Networks is a class of Markovian pure jump processes that model a wide range of phenomena, including chemical reactions at the molecular level, dynamics of wireless communication networks and the spread of epidemic diseases in small populations. There exist exact algorithms that simulate a single path with the exact distribution of the process, but this can be time consuming for high activity processes. Approximate processes, on the other hand, can be used to reduce the computational work, but it may lead to non-physical values and also introduces a time discretization error. 

In this line of research we develop novel hybrid algorithm schemes for simulating these kind of processes, which adaptively switches between exact and approximate methods. These hybrid methods allows us to obtain accurate and computable estimates of the expected value of any smooth observable of the process with nearly optimal computational work.

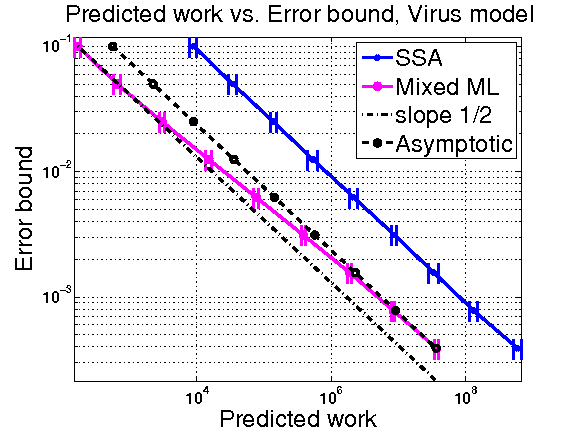
We greately reduced the computational complexity of our first hybrid simulation method by using the Multilevel Monte Carlo methodology and further by introducing an adaptive reaction-splitting method in addition to a general control variate based on the random time-change representation of nonhomogeneous Poisson Processes. Our computational gains are of order O(10^3) in some literature cases.