Multilevel ensemble Kalman filtering

Motivation​

Filtering is a method for sequentially estimating the state of an evolving dynamical system in settings where only partial and possibly inaccurate measurements of the history of the state is available. When working with stochastic models, state estimates are typically given by a probability density conditioned on the measurement data up to the given time; a filtering distribution. For the dynamics of linear Gaussian system, there is a closed form fi ltering distribution solution that is derived via an update formula for its mean and covariance known as the Kalman filter. In general, however, there is no closed form solution, and one must therefore resort to approximation algorithms. 
The Ensemble Kalman Filter (EnKF) is a sequential filtering method that uses an ensemble of particles to estimate means and covariance matrices appearing in the Kalman folter by means of sample moments, i.e., the Monte Carlo method. EnKF is often both a robust and efficient method, but its performance su ffers in settings where the computational cost of accurate simulations of particles is high. The objective of this project is to develop and analyze an extension of the EnKF method that improves the computational efficiency by simultaneously simulating ensemble particles on a hierarchy of accuracy levels.

Methodology

For problems which admit hierarchies of approximations with cost inversely proportional to accuracy, it is natural to leverage solutions to less expensive and less accurate approximations in order to accelerate the convergence of the more expensive and more accurate approximations. The multilevel Monte Carlo (MLMC) is an extension of classical Monte Carlo methods which by sampling stochastic realizations on a hierarchy of resolutions may reduce the computational cost of moment approximations by orders of magnitude. In this project we have combined the ideas of MLMC and EnKF to give rise to the multilevel Ensemble Kalman Filtering method (MLEnKF). MLEnKF is constructed to compute particle paths on a hierarchy of accuracy levels, in this case given by increasing refinement of the temporal discretization, and the Kalman Filter update formulas are extended to multilevel update formulas for means and covariances on the full ensemble hierarchy of particle simulations [1]


Outcome

Theoretical proofs and numerical studies showing that MLEnKF asymptotically approximates filtering distributions orders of magnitude more efficiently than EnKF [1].

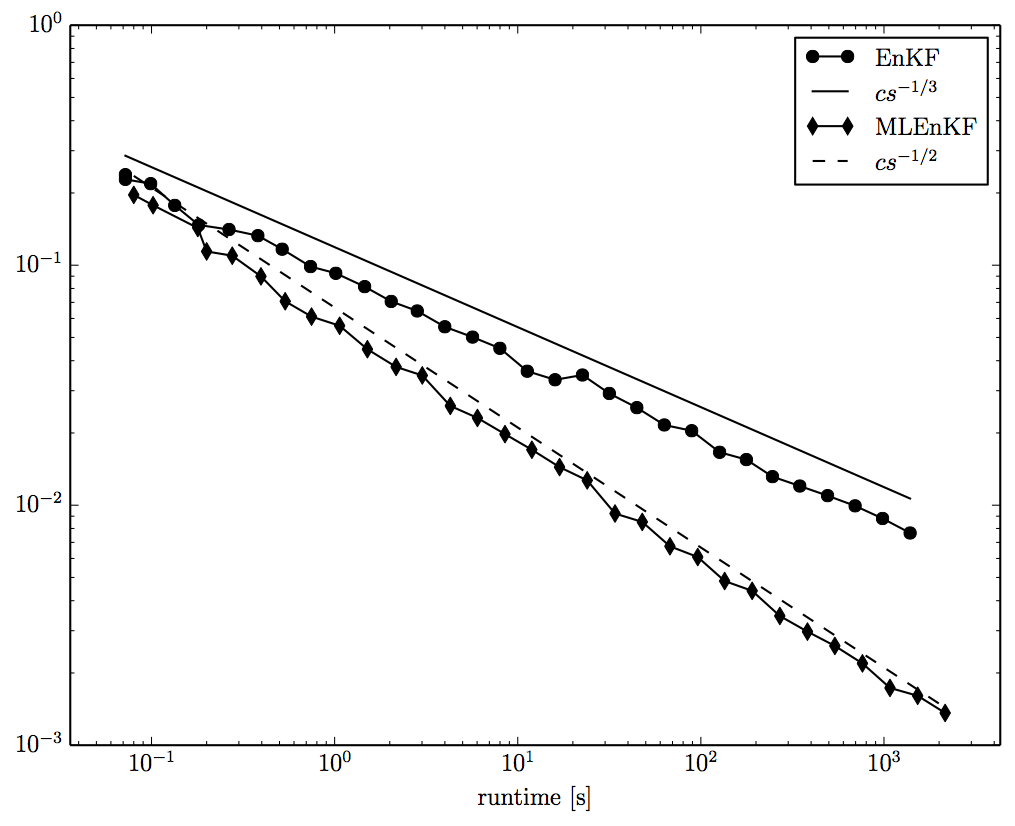
dError-filtering

Figure 1: The error decay for EnKF and MLEnKF as a function of the computational runtime for filtering problem whose underlying dynamics is a Ornstein-Uhlenbeck process. The error is measured in root mean square errors (RMSE) between the exact Kalman filter mean and covariance moments and the corresponding moments from EnKF and MLEnK.

  • Hakon Hoel (University of Oslo)
  • Kody J. H. Law (KAUST)​
  • ​Raul Tempone (KAUST)
[1]​ ​Hoel, H., Law, K. J., and Tempone, R., Multilevel ensemble Kalman fi​ltering, arXiv preprint arXiv:1502.06069, 2015.